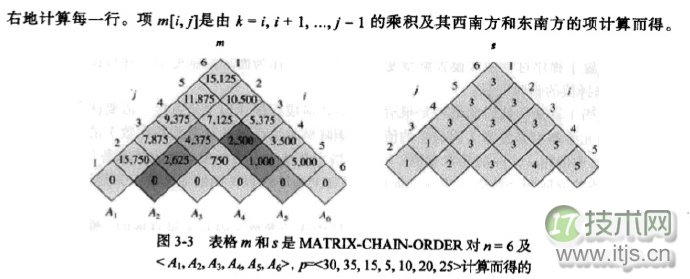
矩阵链乘问题是最典型的动态规划问题,要理解下面的内容请先阅读这篇动态规划的总结。
1.问题描述
矩阵链乘问题的描述如下,就是说要确定一个完全加括号的形式使得矩阵链乘需要进行的标量计算数目最少,矩阵Ai的维数为pi 1×pi,假如穷举所有可能形式的话,时间复杂度是指数级的!因为该问题满足最优子结构,并且子问题存在重叠,所以我们可以借助动态规划来求解。

2.问题分析
我们需要确定一个递归式来将大家要求解的问题表示出来,下面摘自算法导论,介绍地非常详细

最后给出的递归式如下,就是说大家要怎样确定从第i个矩阵到第j个矩阵组成的矩阵链的最优解。假如i和j相等,那么就是一个矩阵,不需要运算;假如i小于j,那么肯定要从它们中间的某个位置分开来,那从哪里分开来呢 这个我们可以尝试下所有可能的选择,也就是尝试不同的位置k,k满足条件(i <= k < j),在位置k将矩阵链进行分开,看看它需要的计算次数,然后我们从这些可能的k中选择使得计算次数最小的那个k进行分开,分开了之后我们的问题就变成了2个小问题,确定矩阵链从i到k 和另一个矩阵链从k+1到j的最优解。假如我们一开始设置i=1(第一个矩阵),j=n(最后一个矩阵),那么,经过上面的递归即可得到我们需要的解。这就是递归的思想!
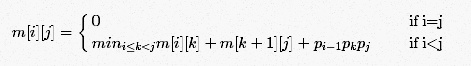
3.代码实现
根据上面的思想我们很快就可以写出一个递归版本的矩阵链承法的实现代码,输出的结果也没有错,给出的加括号的方式是( ( A1 ( A2 A3 ) ) ( ( A4 A5 ) A6 ) )。[问题的数据是算法导论中的问题的数据,值是30,35,15,5,10,20,25]。
def matrixchain_rec(p,i,j):
if i==j:
return 0
for k in range(i,j):
q=matrixchain_rec(p,i,k)+matrixchain_rec(p,k+1,j)+p[i-1]*p[k]*p[j]
if q<m[i][j]:
m[i][j]=q
s[i][j]=k
return m[i][j]
def showmatrixchain(s,i,j):
if i==j:
print 'A%d'%(i),
else:
print '(',
showmatrixchain(s,i,s[i][j])
showmatrixchain(s,s[i][j]+1,j)
print ')',
n=6
p=[30,35,15,5,10,20,25]
m=[[sys.maxint for i in range(n+1)] for j in range(n+1)]
s=[[0 for i in range(n+1)] for j in range(n+1)]
# pprint.pprint(m)
result=matrixchain_rec(p,1,6)
print(result) #15125
showmatrixchain(s,1,6) #( ( A1 ( A2 A3 ) ) ( ( A4 A5 ) A6 ) )
上面的代码运行没有问题,但是,它不够完美!为什么呢 很明显,矩阵链乘问题子问题存在重叠,下面这张图很形象地显示了哪些子问题被重复计算了,所以我们需要改进,改进的方法就是使用带备忘录的递归形式!
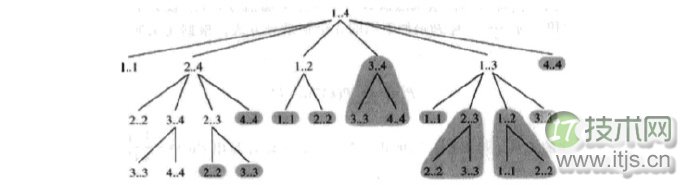
要改成带备忘录的很简单,但是,这次我们不能直接使用原来的装饰器,因为Python中的dict不能对list对象进行hash,所以大家要简单地修改下我们key值的构建,也很简单,看下代码就明白了:
from functools import wraps
def memo(func):
cache={}
@wraps(func)
def wrap(*args):
#build new key!!!
key=str(args[1])+str(args[2])
if key not in cache:
cache[key]=func(*args)
return cache[key]
return wrap
@memo
def matrixchain_rec(p,i,j):
if i==j:
return 0
for k in range(i,j):
q=matrixchain_rec(p,i,k)+matrixchain_rec(p,k+1,j)+p[i-1]*p[k]*p[j]
if q<m[i][j]:
m[i][j]=q
s[i][j]=k
return m[i][j]
def showmatrixchain(s,i,j):
if i==j:
print 'A%d'%(i),
else:
print '(',
showmatrixchain(s,i,s[i][j])
showmatrixchain(s,s[i][j]+1,j)
print ')',
n=6
p=[30,35,15,5,10,20,25]
m=[[sys.maxint for i in range(n+1)] for j in range(n+1)]
s=[[0 for i in range(n+1)] for j in range(n+1)]
# pprint.pprint(m)
result=matrixchain_rec(p,1,6)
print(result) #15125
showmatrixchain(s,1,6) #( ( A1 ( A2 A3 ) ) ( ( A4 A5 ) A6 ) )
接下来的一个问题是,我们怎么实现迭代版本呢 迭代版本关键在于顺序!我们怎么保证我们在计算$A{i…j}的最优解时,所有可能的k的选择需要求解的子问题A{i…k}以及A_{(k+1)…j}$是已经求解出来了的呢 一个简单但是有效的想法就是看矩阵链的长度,我们先计算矩阵链短的最优解,然后再计算矩阵链长的最优解,后者计算时所需要求解的子问题肯定已经求解完了,对不对 于是就有了迭代版本的实现,需要注意的就是其中的i,j,k的取值范围。
import sys
def matrixchain_iter(p):
n=len(p)-1 #total n matrices 6
#to solve the problem below, so initialize to n+1!!!
m=[[0 for i in range(n+1)] for j in range(n+1)]
s=[[0 for i in range(n+1)] for j in range(n+1)]
# for i in range(n): #for matrix with len=1
# m[i][i]=0
# pprint.pprint(m)
for l in range(2,n+1): #iterate the length, max is n
for i in range(1,n-l+2): #i max is n-l+1
j=i+l-1 #j is always l away from i
m[i][j]=sys.maxint #initial to infinity
for k in range(i,j):
#attention to python array when index < 0!!!
#solution is using more space with useless values
q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]
if q<m[i][j]:
m[i][j]=q
s[i][j]=k
# print('when len is %d ' % (l))
# pprint.pprint(m)
return m,s
print('')
m,s=matrixchain_iter(p)
print(m[1][6]) #15125
showmatrixchain(s,1,6) #( ( A1 ( A2 A3 ) ) ( ( A4 A5 ) A6 ) )
实现的时候需要注意一点,在Python中取list中的值时,假如索引是负值的话会从后面往前数返回对应的元素,而以前我们用其他语言的时候肯定是提示越界了,所以代码中用来存储结果的数数组是(n+1)x(n+1),而不是nxn的,这样的话就能够保证返回的是0,而不是从后往前数得到的结果。
得到的数组m如下,m[1,6]就是我们需要的解。
[[0, 0, 0, 0, 0, 0, 0], [0, 0, 15750, 7875, 9375, 11875, 15125], [0, 0, 0, 2625, 4375, 7125, 10500], [0, 0, 0, 0, 750, 2500, 5375], [0, 0, 0, 0, 0, 1000, 3500], [0, 0, 0, 0, 0, 0, 5000], [0, 0, 0, 0, 0, 0, 0]]
数组s如下:
[[0, 0, 0, 0, 0, 0, 0], [0, 0, 1, 1, 3, 3, 3], [0, 0, 0, 2, 3, 3, 3], [0, 0, 0, 0, 3, 3, 3], [0, 0, 0, 0, 0, 4, 5], [0, 0, 0, 0, 0, 0, 5], [0, 0, 0, 0, 0, 0, 0]]
将这个两个数组旋转下,并且只看上三角部分的数字,就可以得到算法导论中给出的那张三角图形了,非常类似杨辉三角