关于二分查找及其上下界问题的一些思考

个人认为在编程的时候，我的代码能力应该是到位的，但是昨天参加的某公司笔试彻底把这个想法给终结了，才意识到自己是多么的弱。其中印象最深刻的是一道关于二分查找上下界的问题。当时洋洋得意，STL 分分钟搞定，结果到了面试的时候他要我自己重新实现一下。这个时候就拙计了，拿着笔的我是写了改改了写，最后勉强算是完成。

今天反思一下，决定自己再把二分查找重新实现一下。也作为给自己的一个警醒，不要总以为自己能力有多高，总有一天会被打脸的。

一、二分查找思想（参照《算法竞赛入门经典》，感谢刘老师）。

在有序表中查找元素常常使用二分查找（Binary Search），有时也译为折半查找，它的基本思想就像是“猜数字游戏”：你在心里想一个不超过1000的正整数，我可以保证在10次以内猜到它—–只要你每次告诉我猜的数比你想的大一些、小一些，或者正好猜中。

猜的方法就是二分。首先我猜500，除了运气特别好正好猜中外，不管你说“太大”还是“太小”，我都可以把可行范围缩小一半：假如“太大”，那么答案在1~499之间，那我下一次猜250；假如“太小”，那么答案在501~1000之间，那我下一次猜750。只要每次选择可行区间的中间点去猜，每次都可以把范围缩小一半。由于log21000 < 10，10次内一定能猜到。

二、STL二分查找

在STL中<algorithm>中已经有二分查找的实现了。我在这里只给简单的应用，也希望读者多去了解一下STL的强大。下面的讲解参照C++ Reference，有兴趣看英文原文的戳链接。

1、binary_search()函数

该函数功能是查看某一值在一个已经排好序的序列中是否存在，当存在时返回true，否则返回false。其函数原型如下：

//default (1)    
template <class ForwardIterator, class T>
  bool binary_search (ForwardIterator first, ForwardIterator last,
                      const T& val);
//custom (2)    
template <class ForwardIterator, class T, class Compare>
  bool binary_search (ForwardIterator first, ForwardIterator last,
                      const T& val, Compare comp);

注意序列是迭代器表示，原则上可以代入多种数据类型。其中几个参数如下：

first：序列需要查询的开始位置；

last：序列需要查询的结束位置；

val：需要查询的元素；

comp：用户自定义比较函数。

注意到default(1)和custom(2)的区别在于用户有没有自定义比较函数。对于default(1)版本，使用运算符 “<” 进行元素间的比较；对于custom(2)，使用用户自定义comp进行元素间比较。

也就是说，binary_search()函数是在序列区间[first, last)中查找是否有某一元素。其中序列一定要先排好序，排序比较函数必须和二分查找比较函数相同。

2、lower_bound()函数

binary_search()只能告诉我们元素在序列中是否存在，却无法定位它的确切位置。并且有时候所给的序列不一定是每个元素都不同的，同值的元素可能多次出现（因为已经排好序，所以相同的元素是相邻的）。假如我们需要找到这些相同的元素中的第一个怎么办？

其实还STL中还定义了lower_bound()函数来解决这个问题，其函数原型如下：

//default (1)    
template <class ForwardIterator, class T>
  ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,
                               const T& val);
//custom (2)    
template <class ForwardIterator, class T, class Compare>
  ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,
                               const T& val, Compare comp);

这个函数的参数和binary_search()函数是相同的，我就不再赘述，但是它的返回类型是ForwardIterator，又见迭代器，为什么不按照我们的要求返回一个整型值表示下表呢？这个我也不解，不过没关系，我们照样能得到我们想要的答案。

也就是说，这个函数的功能是返回迭代器的下界。

确切的说：假如所要查找的元素只有一个，那么lower_lound()返回了这个元素的地址（注意这里是地址，不是下标）；

假如所要查找的元素有多个相同，因为他们相邻，所以可以用一个区间表示[first, last)（左闭右开）它们的位置，那么lower_bound()函数返回的就是first的地址（再次强调是地址）。

3、upper_bound()函数

举一反一，我们大概知道upper_bound()函数是干嘛的了吧，那就是返回迭代器上界，也就是所查找元素的区间的上界，但是和lower_bound()略有不同。

其函数原型如下：

//default (1)    
template <class ForwardIterator, class T>
  ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,
                               const T& val);
//custom (2)    
template <class ForwardIterator, class T, class Compare>
  ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,
                               const T& val, Compare comp);

注意我们之前有强调过，表示相同元素的区间[first, last)是左闭右开的，为什么要这样子？我不知道，你去问问写这套STL的人吧，我不敢黑他。这就造成了lower_bound()和upper_bound()的一个不同之处。那就是：lower_bound()可以相等，upper_bound()不能相等。

更加详细：假如元素只出现一次，那么lower_bound()找到了这个元素的地址，但是upper_bound()找到的却是它的下一个；

假如相同元素出现了多次，那么lower_bound()找到了第一个所找元素的地址，但是upper_bound()找到的却是最后一个元素的下一个元素的地址。

4、简单例子测试。

知道上面的三个函数的使用方法了，那么我们来具体操作一下：

测试代码如下：

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

int main()
{
    int a[] = {0, 0, 2, 2, 2, 4, 4, 4, 4, 5};
    int val;
    while(1)
    {
        printf(“请输入需要查找的数：”);
        scanf(“%d”, &val);
        if(binary_search(a, a+10, val) == false)
            printf(“未找到数 %d，请重新输入!nn”, val);
        else
        {
            printf(“数 %d 已找到!n”, val);
            printf(“相同个数： %dn”, upper_bound(a, a+10, val)-lower_bound(a, a+10, val));
            printf(“下界为：   %dn”, lower_bound(a, a+10, val));
            printf(“上界为：   %dnn”, upper_bound(a, a+10, val));
        }
    }
    return 0;
}

当然上面的是三个函数最简单的应用了，为了让大家看得更清楚，读者不要喷我一个函数写了多次。我们可以查看所找元素是否存在，它第一次出现的位置和最后一次出现的位置，同时我们看知道了上下界就可以求出该元素出现了多少次。但是，我们看测试结果:

对，我们没有看错，这个上下界是地址。就拿2来看，上界减下界等于12，一个int型占用4个字节，那么2的个数为3个。但是，大家要地址干什么？没有用啊！

别着急，想得到下标还不简单。稍稍修改一下：

    printf("下界为：   %dn", lower_bound(a, a+10, val)-a);     //减去首地址，就找到了下标位置
    printf("上界为：   %dn", upper_bound(a, a+10, val)-a);   //同上
    printf("该元素所在范围： [%d, %d)nn", lower_bound(a, a+10, val)-a, upper_bound(a, a+10, val)-a);

程序运行结果如图：

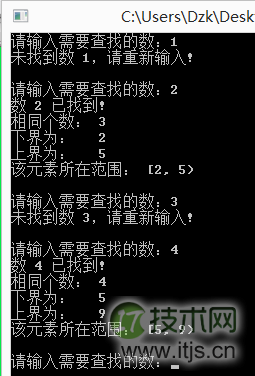
至此，STL二分查找的三个函数大致介绍完成，还有另外的几个函数读者有兴趣可以上C++ Reference去挖掘一下。

三、手动实现二分查找三个函数。

本来今天的重点应该放在我是怎么实现上的，不知道怎么就跑偏了。其实讲了思想，大家应该可以着手写代码了。不同人有不同人实现的方法，其中的技巧还是有不少的。下面给处我个人的实现，假如有人能挑出其中的缺陷，欢迎点评。

1、binary_search()函数

STL的binary_search()返回的是bool值，不过一般算法书或者数据结构书上都是这样阐述的：若找到，输出它的下标，若未找到，输出-1。

下面呢，是我的简单实现，功能如上所述：

#include <iostream>
#include <cstdio>
using namespace std;

int binary_search_1(int* A, int l, int r, int val)    //A为序列，l为左边界，r为右边界，val是元素
{
    //cout << l << " " << r << endl;
    if(l > r) return -1;                    //左边界严格不大于右边界，否则说明找不到
    int mid = l+(r-l)/2;                    //从中剖分，注意这里的一个小技巧，为何不用(l+r)/2，读者可以去思考,下面函数的注释会给出解答。
    if(A[mid] == val) return mid;           //假如找到，返回
    if(A[mid] > val) r = mid-1;       //否则，修改边界
    else l = mid+1;
    return binary_search_1(A, l, r, val);     //递归调用
}
int main()
{
    int a[] = {0, 0, 2, 2, 2, 4, 4, 4, 4, 5};
    cout << binary_search_1(a, 0, 10, 2);  //a为数组，0为起始位置，9为结束位置，表明你要查找的特定区间，现在为0~9，2为元素
    return 0;
}

下面看非递归版的：

int binary_search_2(int* A, int l, int r, int val)    //A为序列，l为左边界，r为右边界，val是元素
{
    int mid;
    while(l < r)
    {
        mid = l+(r-l)/2;
        if(A[mid] == val) return mid;
        if(A[mid] > val) r = mid-1;
        else l = mid+1;
    }
    return -1;
}

2、lower_bound()函数和upper_bound()函数

自己实现的binary_search()在元素都互不相同的时候还挺好，但是假如存在相同元素时，那就存在不确定性，那么，它具体返回哪一个呢，这是不确定的。那么我们来实现一下lower_bound()函数，求一下它的下界，既然是自己实现，就可以把下标输出来了，规避掉地址。

代码如下，参数与binary_search()相同：

#include <iostream>
#include <cstdio>
using namespace std;

int lower_bound_1(int* A, int l, int r, int val)    //二分求下界
{
    //cout << "l and r: " << l << " " << r << endl;
    if(l > r) return -1;
    if(A[l] == val) return l;
    int mid = l+(r-l)/2;         //注意这里是l+(r-l)/2，当l+r是奇数时，mid它是更靠近l
    if(A[mid] > val) r = mid-1;
    else if( A[mid] == val) r = mid;
    else l = mid+1;
    return lower_bound_1(A, l, r, val);     //递归调用
}

int upper_bound_1(int* A, int l, int r, int val)    //二分求上界
{
    //cout << "l and r: " << l << " " << r << endl;
    if(l > r) return -1;
    if(A[r] == val) return r;
    int mid = l+(r-l+1)/2;      //注意这里是l+(r-l+1)/2，当l+r是奇数时，mid它是更靠近r
    if(A[mid] > val) r = mid-1;
    else if( A[mid] == val) l = mid;
    else l = mid+1;
    return upper_bound_1(A, l, r, val);     //递归调用
}

int main()
{
    int a[] = {0, 0, 2, 2, 2, 4, 4, 4, 4, 5};
    printf("lower_bound at %dn", lower_bound_1(a, 0, 9, 4));
    printf("upper_bound at %dn", upper_bound_1(a, 0, 9, 4));
    return 0;
}

非递归代码：

int lower_bound_2(int* A, int l, int r, int val) //非递归版本，参数设置三个函数都相同
{
    int mid;
    while(l < r)
    {
        mid = l+(r-l)/2;
        if(A[mid] > val) r = mid-1;
        else if(A[mid] == val) r = mid;
        else l = mid+1;
    }
    if(A[l] == val) return l;
    return -1;
}

int upper_bound_2(int* A, int l, int r, int val) //非递归版本，参数设置三个函数都相同
{
    int mid;
    while(l < r)
    {
        mid = l+(r-l+1)/2;
        if(A[mid] > val) r = mid-1;
        else if(A[mid] == val) l = mid;
        else l = mid+1;
    }
    if(A[r] == val) return r;
    return -1;
}

3、测试

自己已经在机器上测试了一遍，写测试函数好累，读者有兴趣自己测试吧。偷个懒。

四、总结

二分查找的算法效率是非常非常高的，我相信我在这里讲的应该挺详细了。下面有一道题就要用到二分的思想。

题目：

正整数数组a[0], a[1], a[2], ···, a[n-1]，n可以很大，大到1000000000以上，但是数组中每个数都不超过100。现在要你求所有数的和。假设这些数已经全部读入内存，因而不用考虑读取的时间。希望你用最快的方法得到答案。

提示：二分。